📢 LLM 真的可以在數學中跳出框框進行推理嗎？或者他們只是重新混合了熟悉的策略？ 請記住 DeepSeek R1，o1 在奧林匹克級別的數學上給我們留下了深刻的印象，但他們在簡單的算術😬上也失敗了 我們建立了一個基準測試來瞭解 → OMEGA Ω 📐 💥 我們發現，儘管 RL 非常強大，但它難以組合技能和創新訓練期間沒有看到的新策略。👇 與 @UCBerkeley @allen_ai合作 關於我們學到🧵的內容的帖子

🤯 我們注意到，許多失敗不是因為缺乏知識，而是因為想得太多。模型通常在 CoT 的早期找到正確的答案，但會螺旋式地陷入自我糾正並放棄正確的解決方案。這挑戰了以下假設： 更多的 CoT ≠更好的結果 有時，模型的自我糾正機制可能會無意中適得其反

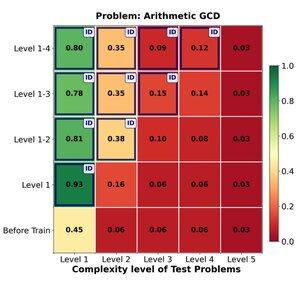
🔁 RL 能否有效地從易問題推廣到難問題？我們發現早期收益強勁，但泛化平臺期與任務複雜性較高 1-4 級的訓練對域內問題有很大的提升，例如 1 級（ 📈 RL 後為 0.45 → 0.80）。 但是當我們增加難度 📉 同一問題系列的性能下降。 ⚠️ 學習策略的延伸程度是有限的

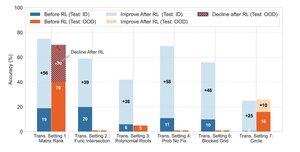
🧠 變革性的概括？ 仍然遙不可及。當成功取決於發明一種新的解決方案策略（例如，巧妙的對稱性而不是蠻力）時，即使在 RL 之後，模型也總是失敗的。 RL 可以顯著提高遵循訓練期間觀察到的熟悉模式的任務的性能，當成功取決於數據中未明確證明的創造性洞察力或推理策略時，它會很掙扎。