📢 ¿Pueden realmente los LLMs razonar fuera de lo común en matemáticas? ¿O solo están remixando estrategias familiares? Recuerda que DeepSeek R1, o1 nos impresionaron en matemáticas a nivel de Olimpiada, pero también fallaron en aritmética simple 😬 Construimos un benchmark para averiguarlo → OMEGA Ω 📐 💥 Descubrimos que, aunque son muy poderosos, los RL tienen dificultades para componer habilidades e innovar nuevas estrategias que no se vieron durante el entrenamiento. 👇 trabajamos con @UCBerkeley @allen_ai Un hilo sobre lo que aprendimos 🧵

🤯 Nos dimos cuenta de que muchos fracasos no provienen de la falta de conocimiento, sino de pensar en exceso. Los modelos a menudo encuentran la respuesta correcta al principio en CoT, pero entran en una espiral de autocorrecciones y abandonan soluciones correctas. Esto desafía la suposición: Más CoT ≠ mejores resultados A veces, los mecanismos de autocorrección de los modelos pueden, sin querer, salir mal.

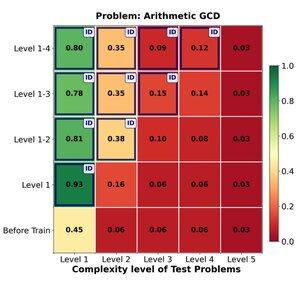
🔁 ¿Puede el aprendizaje por refuerzo (RL) generalizar efectivamente de problemas fáciles a difíciles? Encontramos fuertes ganancias tempranas, pero la generalización se estanca con la complejidad de la tarea. Entrenar en los niveles 1–4 proporciona un sólido impulso en problemas dentro del dominio, por ejemplo, en el nivel 1 (📈 0.45 → 0.80 después de RL). PERO cuando aumentamos la dificultad 📉 el rendimiento cae en la misma familia de problemas. ⚠️ Hay límites en cuánto pueden estirarse las estrategias aprendidas.

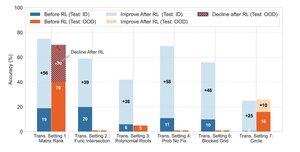
🧠 ¿Generalización transformadora? Aún fuera de alcance. Cuando el éxito depende de inventar una nueva estrategia de solución (por ejemplo, simetría ingeniosa en lugar de fuerza bruta), los modelos fallan consistentemente incluso después del aprendizaje por refuerzo. El aprendizaje por refuerzo puede mejorar sustancialmente el rendimiento en tareas que siguen patrones familiares observados durante el entrenamiento, pero tiene dificultades cuando el éxito depende de la percepción creativa o estrategias de razonamiento que no se demuestran explícitamente en los datos.