📢 Czy LLM-y naprawdę potrafią myśleć nieszablonowo w matematyce? A może tylko remiksują znane strategie? Pamiętajcie o DeepSeek R1, o1, które zaimponowały nam na poziomie matematyki olimpijskiej, ale również zawiodły w prostych działaniach arytmetycznych 😬 Stworzyliśmy benchmark, aby to sprawdzić → OMEGA Ω 📐 💥 Odkryliśmy, że chociaż są bardzo potężne, RL ma trudności z łączeniem umiejętności i innowowaniem nowych strategii, które nie były widziane podczas treningu. 👇 pracuj z @UCBerkeley @allen_ai Wątek o tym, czego się nauczyliśmy 🧵

🤯 Zauważyliśmy, że wiele niepowodzeń wynika nie z braku wiedzy, ale z nadmiernego myślenia. Modele często znajdują prawidłową odpowiedź na początku CoT, ale wpadają w spiralę samokorekcji i porzucają poprawne rozwiązania. To kwestionuje założenie: Więcej CoT ≠ lepsze wyniki Czasami mechanizmy samokorekcji modeli mogą nieumyślnie przynieść odwrotny skutek.

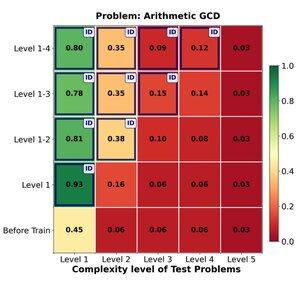
🔁 Czy RL może skutecznie uogólniać z łatwych na trudne problemy? Odkrywamy silne wczesne zyski, ale uogólnienie osiąga plateau wraz ze wzrostem złożoności zadania. Trening na poziomach 1–4 daje solidny wzrost w problemach wewnętrznych, np. na poziomie 1 (📈 0.45 → 0.80 po RL). ALE gdy zwiększamy trudność 📉 wydajność spada w tej samej rodzinie problemów. ⚠️ Istnieją ograniczenia, jak daleko można rozciągnąć wyuczone strategie.

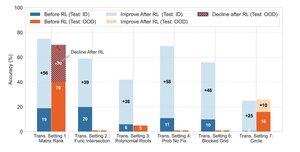
🧠 Transformacyjna generalizacja? Wciąż poza zasięgiem. Gdy sukces zależy od wynalezienia nowej strategii rozwiązania (np. sprytna symetria zamiast siły brute force), modele konsekwentnie zawodzą nawet po RL. RL może znacznie poprawić wydajność w zadaniach, które podążają za znanymi wzorcami obserwowanymi podczas treningu, ale ma trudności, gdy sukces zależy od kreatywnego wglądu lub strategii rozumowania, które nie zostały wyraźnie przedstawione w danych.