📢 Será que os LLMs conseguem realmente raciocinar fora da caixa em matemática? Ou estão apenas remixando estratégias familiares? Lembre-se do DeepSeek R1, o1 nos impressionou em matemática de nível Olimpíada, mas também falhou em aritmética simples 😬 Construímos um benchmark para descobrir → OMEGA Ω 📐 💥 Descobrimos que, embora sejam muito poderosos, os RL têm dificuldades em compor habilidades e inovar novas estratégias que não foram vistas durante o treinamento. 👇 trabalhe com @UCBerkeley @allen_ai Um fio sobre o que aprendemos 🧵

🤯 Notámos que muitas falhas não decorrem da falta de conhecimento, mas sim do excesso de reflexão. Os modelos muitas vezes encontram a resposta certa cedo no CoT, mas entram em espirais de autocorreções e abandonam soluções corretas. Isso desafia a suposição: Mais CoT ≠ melhores resultados Às vezes, os mecanismos de autocorreção dos modelos podem, inadvertidamente, ter o efeito oposto.

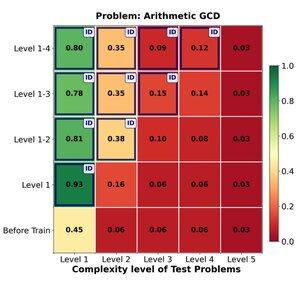
🔁 A RL pode efetivamente generalizar de problemas fáceis para difíceis? Encontramos fortes ganhos iniciais, mas a generalização atinge um platô com a complexidade da tarefa. Treinar nos níveis 1–4 dá um impulso sólido em problemas dentro do domínio, por exemplo, no nível 1 (📈 0.45 → 0.80 após RL). MAS quando aumentamos a dificuldade 📉 o desempenho cai na mesma família de problemas. ⚠️ Existem limites para até onde as estratégias aprendidas podem se estender.

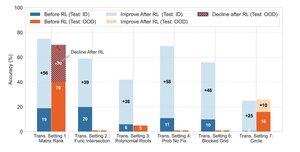
🧠 Generalização transformadora? Ainda fora de alcance. Quando o sucesso depende da invenção de uma nova estratégia de solução (por exemplo, simetria inteligente em vez de força bruta), os modelos falham consistentemente mesmo após o RL. O RL pode melhorar substancialmente o desempenho em tarefas que seguem padrões familiares observados durante o treinamento, mas tem dificuldades quando o sucesso depende de insights criativos ou estratégias de raciocínio não explicitamente demonstradas nos dados.