Popularne tematy
#
Bonk Eco continues to show strength amid $USELESS rally
#
Pump.fun to raise $1B token sale, traders speculating on airdrop
#
Boop.Fun leading the way with a new launchpad on Solana.
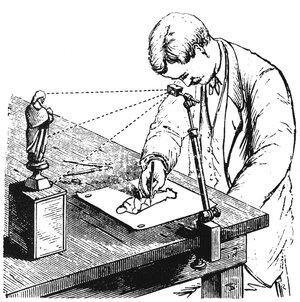
"Camera lucida" to urządzenie, które wykorzystuje pryzmat trzymany przez metalową ramę do projekcji obrazu sceny przed nim na kartkę papieru poniżej, trochę jak nowoczesny projektor podłączony do strumienia wideo z kamery na żywo.
Prawdopodobnie zostały wynalezione na początku lat 1400, chociaż opublikowane relacje na ich temat pojawiają się dopiero pod koniec lat 1500. Częściowo powodem tego może być to, że były ściśle strzeżonymi tajemnicami handlowymi artystów, którzy używali ich, aby osiągnąć stopień dokładności, który wcześniej był niemożliwy lub przynajmniej niezwykle trudny do osiągnięcia w „rysunku odręcznym” bez pomocy.
Artysta David Hockney zainteresował się tym tematem wiele lat temu i napisał na ten temat książkę w 2001 roku. Jego podstawowa teoria głosiła, że niezwykła poprawa w dokładności i realizmie była bezpośrednio przypisywana tajnemu użyciu camera lucida (a także wcześniejszego urządzenia zwanego camera obscura).
Jak zauważył, przed tym okresem nigdy nie widziałeś obrazu lutni w perspektywie, który nie wyglądałby na zniekształcony i błędny. Choć można było użyć „reguł perspektywy”, aby realistycznie narysować proste kształty prostokątne, bardziej złożona geometria lutni była poza normalnymi ludzkimi możliwościami realistycznego przedstawienia w przestrzeni. Ta teoria jest znana jako teza Hockney'ego-Falco.
Od kiedy dowiedziałem się o tym na studiach na początku lat 2000, w pewien sposób mentalnie zastosowałem gwiazdkę do prac niektórych malarzy. Na przykład, tak bardzo jak szanuję i podziwiam Ingres'a i Caravaggia, podziw, jaki miałem dla ich umiejętności, był osłabiony przez uświadomienie sobie, że prawdopodobnie korzystali z tego rodzaju mechanicznej pomocy.
I oczywiście, wiele sztuki tkwi w koncepcji, kompozycji i kadrowaniu, kolorach, pociągnięciach pędzla itd. Ale to zapierające dech w piersiach, realistyczne odwzorowanie najbardziej mnie imponowało, a ta część została przynajmniej częściowo zniszczona przez to odkrycie. To również sprawiło, że jeszcze bardziej szanowałem rzeźbiarską realizm Michała Anioła (a także jego studia, które są wyraźnie szkicami wykonanymi z natury).
W każdym razie, powód, dla którego poruszam ten temat teraz, to to, że wierzę, iż stoimy na progu podobnego zjawiska w dziedzinach badań matematycznych z nadejściem modeli takich jak GPT-5 Pro.
Już użyłem go do tego, co podejrzewam, że jest naprawdę nowym i interesującym badaniem (jak szczegółowo opisałem w ostatnich wątkach), a dzisiaj otrzymaliśmy aktualizację od Sebastiena Bubecka z OpenAI, pokazującą, że model był w stanie udowodnić interesujący wynik w współczesnej matematyce, używając nowego dowodu, w jednym podejściu, co najmniej.
Więc ta nowa era nagle nadeszła. W zeszłym tygodniu zobaczyliśmy wynik od chińskich naukowców komputerowych, którzy pobili rekord w optymalnym sortowaniu, który utrzymywał się przez 45 lat.
W tym czasie zastanawiałem się, czy AI zostało w jakiś sposób użyte do wygenerowania tego wyniku.
Zobacz także niedawny artykuł w cytowanym tweecie, który ma podobny charakter, ponieważ jest zarówno zaskakujący, jak i elementarny. Te wyniki wydają mi się być cechami, które mogły skorzystać z AI w jakiś sposób.
Nie chcę oskarżać tych autorów o nic. Z tego, co wiem, zrobili wszystko ręcznie, tak jak malarze w latach 1300.
A nawet jeśli użyli AI, aby im pomóc, nie mamy jeszcze zaakceptowanych norm dotyczących tego, jak się z tym obchodzić: jakie ujawnienia są uzasadnione i jak należy podzielić i rozważyć uznanie. Cała koncepcja autorstwa musi być dzisiaj na nowo przemyślana.
W moim ostatnim wątku, w którym badałem wraz z GPT-5 Pro zastosowanie teorii Lie w głębokim uczeniu, sam opracowałem podpowiedzi, chociaż nigdy w milionie lat nie byłbym w stanie wygenerować teorii i kodu, które model opracował w wyniku tych podpowiedzi. Czy dostanę uznanie za ten wynik, jeśli okaże się, że zrewolucjonizuje dziedzinę?
Co z moim kolejnym eksperymentem, w którym użyłem moich oryginalnych podpowiedzi, które napisałem samodzielnie, wraz z „meta podpowiedzią”, aby skłonić GPT-5 Pro do wymyślenia 10 kolejnych par podpowiedzi, luźno wzorowanych na moich własnych, ale dotyczących zupełnie innych gałęzi matematyki, które rozwijały się w zupełnie innych kierunkach.
...
Najlepsze
Ranking
Ulubione













